Introduction
Many real-world, multi physical systems involving fluids are governed by scalar and vector transport equations. Further, systems involving multiple phases of fluids, fluid-structure interactions etc. can be formulated into mathematical problems using such equations and the appropriate boundary conditions. Such problems can generally be solved using computational methods. At certain regimes, these field equations/boundary conditions can be linearized (Ex. Low Reynolds number hydrodynamics, Low Peclet number mass transport etc.), and problems founded in these regimes can be treated analytically using a plethora of established mathematical techniques. Interfacial fluid mechanics is a subset of the above ideas that is used to handle problems wherein the dynamics and the rheology of fluid interfaces play a significant role in determining the behavior of the system. (Ex. The dynamics of drops and bubbles in the presence of surfactants, free surface dynamics of thin films, etc.)
Our Research
Colloidal motors are particles capable of converting certain types of energy (chemical, thermal etc.) into mechanical motion. They are capable of self-propulsion at scales where the absence of inertia disallows traditional swimming mechanisms (From “Purcell’s theorem”). However, existing designs for colloidal motors suffer from various difficulties including low propulsion speeds, poor control near boundaries, etc. New designs of colloidal motors are necessary to circumvent these limitations. Surface tension-based mechanisms can provide a suitable alternative to the existing techniques (Diffusiophoresis, Thermo/Electrophoresis etc.)
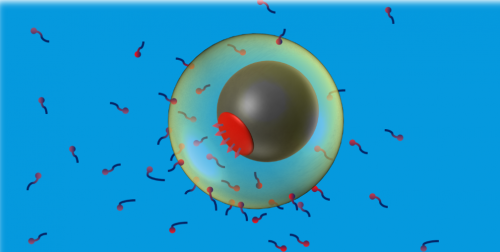
Figure 1: Illustrative diagram of compound drop-Janus particle system designed to generate a flux of surface-active species from its Janus cap.
